Powering 170v tubes from the wall
So I’ve been working on how to power nixie tubes in the simplest way, getting 170v isn’t as easy as connecting a wall-wart and using an LDO.  There are lots of boost circuits to go from 5v or 12v up to ~170v, but there are tons of options, can be a little on the expensive and some include a bunch of extra components which I don’t really want to deal with.  I decided to investigate powering the tubes from the rectified 120vac mains.
US mains AC is 120v RMS, which means using a full-bridge rectifier would result in a peak voltage of 170vdc [RMS and and full bridge rectifier].  Adding a capacitor to the output would hold the voltage at the peak of 170vdc.  As power is used from the capacitor it is replenished to 170v at a rate of 120Hz, resulting a 120Hz ripple voltage.  The tubes only use 2.5 mA each, so with a total of  15mA of draw I figured a little DF04 bridge rectifier and a 200v 10uF cap should work just fine.  I made up a little test board last night and hooked up a scope today.
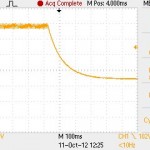
Looks like with a 20mA draw there is about 14v of ripple, the min voltage is 158v (above the cut off for the tubes) and the drain time once power is pulled is ~300ms, which means the cap won’t be charged to 170v for too long.
Now I just need to figure out a way to get down to 5v from the mains without a gigantic transformer
3 Comments
Other Links to this Post
RSS feed for comments on this post. TrackBack URI

By billy h, December 19, 2012 @ 5:41 am
Hey greAt idea thanks for posting it.im trying to find schematic of how to rectify mains using a 50L6 tube.for powering a 12 a 12at7 .but no luck.. i know it can be done cuz i got to old heathkit radios that are tranformerless. I may just copy there design but i want to make my own regen radio. But dont want to flip for a trans former.there is a book series called impoverished radio experimenter. In book one the have a power supply that uses two readily available low voltage transfkrmers. Hooked to each others primarys.but then i still dont want a transformer.the books are available from lindsay publications peace from Oklahoma city
By jbb, October 18, 2013 @ 3:41 am
Nice, simple idea. Can I just suggest a couple of little enhancements?
1) A 200V cap running at 170V might have a short lifetime, especially if warm. A 250V cap would have a good margin.
2) A 20R – 100R series resistor would reduce the capacitor inrush current and could save you some trouble.
3) A fuse is always a good idea when directly connecting to the mains.
By s1axter, October 18, 2013 @ 8:14 am
Thanks jbb, yes using a bigger cap would increase the life of the system. And I totally agree, fuse anything coming out of the wall!